1) Find the perimeters of the square and the triangle.
Suppose you divide the wire into 2 pieces that measure x and y. x is used to make the square and y is used to make the triangle, according to the figure:
x is the perimeter of the square;
y is the perimeter of the triangle.
Since the total wire is 30 inches long:
x + y = 30 (equation 1).
2) Find the area of the geometric figures.
Square:
Since a square has 4 equal sides, each side will measure x/4 (4*x/4=x)
And, since the area (As) of a square whose side measures a is:
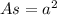
The area of the square is:
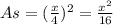
Equilateral Triangle:
Since an equilateral triangle has 3 equal sides, each side will measure y/3 (3*y/3 = y).
And, since the area (At) of an equilateral triangle whose side measures b is:
![At=\frac{\sqrt[]{3}}{4}\cdot b^2](https://img.qammunity.org/2023/formulas/mathematics/high-school/stv3cgp2y0rxs5ljpyjjkmvm8wvamtfexo.png)
The area of the triangle is:
![\begin{gathered} At=\frac{\sqrt[]{3}}{4}\cdot((y)/(3))^2 \\ At=\frac{\sqrt[]{3}}{4}\cdot(y^2)/(9)=\frac{\sqrt[]{3}}{36}\cdot y^2 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/3umnmmnaef99dp9t0aom0d1vmnbhkbhxit.png)
3) Find the total area.
The total area (A) is the sum of the areas:
![\begin{gathered} A=As+At \\ A=(x^2)/(16)+\frac{\sqrt[]{3}}{36}\cdot y^2 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/9in0xfer4q5g8kxsph8ae9csxd7cvcalny.png)
4) Isolate y in equation 1 and substitute in the equation for the area.
x + y = 30
y = 30 - x
![A=(x^2)/(16)+\frac{\sqrt[]{3}}{36}\cdot(30-x)^2](https://img.qammunity.org/2023/formulas/mathematics/high-school/rr2cjoj7tvg9uccso5qnoxof2ctmclbkig.png)
5) The maximum or minimum value of A happens at x when dA/dx = 0.
So, derivate A:
![\begin{gathered} (dA)/(dx)=(2x)/(16)+\frac{\sqrt[]{3}}{36}\cdot(30-x)\cdot2\cdot(-1) \\ (dA)/(dx)=(x)/(8)-\frac{\sqrt[]{3}}{18}(30-x) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/y7u0b0k67p11iq80a8khdpybifd3ypu9oj.png)
And do dA/dx = 0 to find x.
![0=(x)/(8)-\frac{\sqrt[]{3}}{18}(30-x)](https://img.qammunity.org/2023/formulas/mathematics/high-school/nyvyfhzvaq69rp7i7cjisagds6febk2fhf.png)
Then, isolate x:
![\begin{gathered} 0=(x)/(8)-\frac{\sqrt[]{3}}{18}\cdot30+\frac{\sqrt[]{3}}{18}\cdot x \\ \frac{\sqrt[]{3}}{18}\cdot30=(x)/(8)+\frac{\sqrt[]{3}}{18}\cdot x \\ 2.89=0.3x \\ x=(2.89)/(0.22) \\ x=13 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/8eh9vm8agyxwfj1mabdcn1upodylpd9s3x.png)
6) Evaluate the equation for x at the exremes x = 0; y = 30, and at x = 13.
For x = 0
![\begin{gathered} A=(x^2)/(16)+\frac{\sqrt[]{3}}{36}\cdot(30-x)^2 \\ (0^2)/(16)+\frac{\sqrt[]{3}}{36}\cdot(30-0)^2 \\ =\frac{\sqrt[]{3}}{36}\cdot900 \\ =43.3 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/ts8p59p7p2yspudvkodvgjt3bwcayfr4mn.png)
For x = 30
![\begin{gathered} A=(x^2)/(16)+\frac{\sqrt[]{3}}{36}\cdot(30-x)^2 \\ A=(30^2)/(16)+\frac{\sqrt[]{3}}{36}\cdot(30-30)^2 \\ =(900)/(16)+\frac{\sqrt[]{3}}{36}\cdot0 \\ =56.25 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/rv6zc1prl6cq710lcfe85lhrfl330nzcqu.png)
And for x =13
![\begin{gathered} A=(13^2)/(16)+\frac{\sqrt[]{3}}{36}\cdot(30-13)^2 \\ A=(169)/(16)+\frac{\sqrt[]{3}}{36}\cdot17^2 \\ A=(169)/(16)+\frac{\sqrt[]{3}}{36}\cdot289 \\ A=24.47 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/6sx6yc224htvceq573yu1xd66p8j2in9sp.png)
7) Compare the results:
As you can see in step 6, when x = 13, the area is minimized, while the area is maximized when x = 30.
The greatest area will be reached when x = 30. That means y = 0 (x + y =30).
Answer:
The greatest area is reached when all the wire is used to make the square.
To make the 2 figures, we wire should be cut as nearest as possible to 30, and the greatest piece should be used to make the square.