Question

Find lateral surface area and volume of the solid object(Round to nearest whole number as needed)

Answer 1

`\begin{gathered} \text{LSA}\approx312m^2 \\ V\approx794m^3 \end{gathered}`

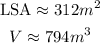
1) Note that this solid, is a cross-sectioned cone. We can find the Lateral Surface Area, using this formula:

`LSA=\pi\cdot s\cdot(R+r)_{}`

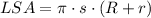
Where R, is the biggest radius, s for the slant height, r for the smallest radius.

2) So, plugging the measures into that we can write out:

`\text{LSA}=\pi\cdot9.63(6.20+4.10)=311.61m^2\approx312m^2`

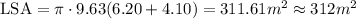
Note that we have rounded it off to the nearest whole. So now, let's find the volume of that solid:

`V=(\pi h)/(3)(R^2+Rr+r^2)`

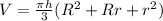
Plugging into that the given dimensions:

`\begin{gathered} V=(\pi h)/(3)(R^2+Rr+r^2) \\ V=(\pi\cdot9.4)/(3)(6.2^2+6.2\cdot4.1+4.1^2) \\ V\approx794m^3 \end{gathered}`

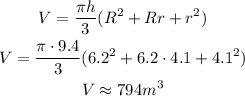
Note the volume in cubic meters.

And that is the answer