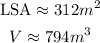
1) Note that this solid, is a cross-sectioned cone. We can find the Lateral Surface Area, using this formula:
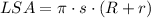
Where R, is the biggest radius, s for the slant height, r for the smallest radius.
2) So, plugging the measures into that we can write out:
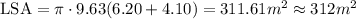
Note that we have rounded it off to the nearest whole. So now, let's find the volume of that solid:
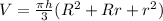
Plugging into that the given dimensions:
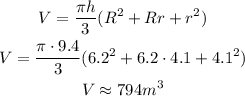
Note the volume in cubic meters.
And that is the answer