We need to solve the following expression:
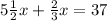
To find which steps are possible we will solve the equation one step at a time and check which of these steps appear on the options.
The first step is to transform the mixed fraction into a improper fraction, we do that by adding the integer part wih the fraction part.

The second step is to find the LCM of the two fractions and add them.
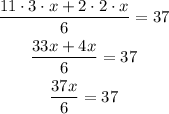
The third step is to multiply both sides by 6.

The fourth step is to divide both sides by 37.

The first, second and fourth step appear on the options. Therefore we should marke the option "x=6", the option "37/6 x=37" and the option "11/2 x + 2/3 x= 37".