In this problem we have a normal distribution with:
• μ = mean = 100,
,
• σ = standard deviation = 15.
(a) The z-score for a value x = 124 is:
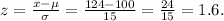
(b) We must compute the probability that x is greater than 124, which is equivalent to the probability of having z greater than 1.6. Using a table of z-score, we find that:

Answer
• (a), z = 1.6
,
• (b), P(x > 124) = 0.0548