Question

Find both the number combinations in the number of permutations for 9 objects taken 7 at a time

Answer 1

The number of permutations for 9 objects taken 7 at a time is 181440.

Finding both the number combinations in the number of permutations

From the question, we have the following parameters that can be used in our computation:

9 objects taken 7 at a time

The number of permutations for 9 objects taken 7 at a time using the following formula:

`^nP_r = (n!)/((n - r)!)`

So, we have

`^9P_7 = (9!)/(2!)`

Evaluate

`^9P_7 = 181440`

Hence, the number of permutations for 9 objects taken 7 at a time is 181440.

Answer 2

There are 36 combinations and 181440 permutations

Step-by-step explanation

The number of combinations of n object taking r at a time is given by the formula;

`^nC_r=(n!)/(r!(n-r)!)`

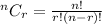
From the question, n = 9 and r = 7, then substitute these values into the formula

`^9C_7=(9!)/(7!(9-7)!)=\frac{9!}{7!\text{ }2!}=(9\cdot8\cdot7!)/(7!*2)=(72)/(2)=36`

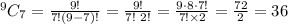
The number of permutations of n object taking r at a time is given by the formula;

`^nP_r=(n!)/((n-r)!)`

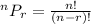
Also, n = 9 and r = 7, then substitute these values into the formula to get the number of permutations

`^9P_7=(9!)/((9-7)!)=(9!)/(2!)=(9\cdot8\cdot7\cdot6\cdot5\cdot4\cdot3\cdot2!)/(2!)=181440`

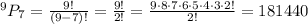
Therefore, there are 36 combinations and 181440 permutations