Answer
There are 36 combinations and 181440 permutations
Step-by-step explanation
The number of combinations of n object taking r at a time is given by the formula;
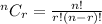
From the question, n = 9 and r = 7, then substitute these values into the formula
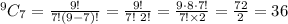
The number of permutations of n object taking r at a time is given by the formula;
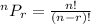
Also, n = 9 and r = 7, then substitute these values into the formula to get the number of permutations

Therefore, there are 36 combinations and 181440 permutations