SOLUTION
Given the question in the image, the following are the solution steps to answer the question.
STEP 1: Describe the Emperical rule
The Empirical Rule(68-95-99.7 Rule) states that, for a normally distributed random variable:
68% of the measures are within 1 standard deviation of the mean.
95% of the measures are within 2 standard deviation of the mean.
99.7% of the measures are within 3 standard deviations of the mean.
STEP 2: Write the given details
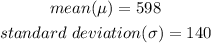
STEP 3: Solve the question
In this problem, we have that:

So 318 is 2 standard deviations below the mean.
So 878 is 2 standard deviations above the mean.
The EMPIRICAL RULE (or the 68-95-99.7 Rule) says that about 68% of the data is between 1 standard deviation below the mean and 1 standard deviation above the mean. Below the shaded part is about 68% of the area between the normal curve and the z-axis.
The EMPIRICAL RULE (or the 68-95-99.7 Rule) also says that about 95% of the data is between 2 standard deviations below the mean and 2 standard deviations above the mean. Below the shaded part is about 95% of the area between the normal curve and the z-axis.
Going by this descriptions above, this means that:
The percentage of people taking the test who score between 318 and 878 is 95%