Question

Scores on the GRE (Graduate Record Examination)are normally distributed with a mean of 598 and astandard deviation of 140. Use the 68-95-99.7 Ruleto find the percentage of people taking the test whoscore between 318 and 878.The percentage of people taking the test who scorebetween 318 and 878 is _ %

Answer 1

Given the question in the image, the following are the solution steps to answer the question.

STEP 1: Describe the Emperical rule

The Empirical Rule(68-95-99.7 Rule) states that, for a normally distributed random variable:

68% of the measures are within 1 standard deviation of the mean.

95% of the measures are within 2 standard deviation of the mean.

99.7% of the measures are within 3 standard deviations of the mean.

STEP 2: Write the given details

`\begin{gathered} mean(\mu)=598 \\ standard\text{ }deviation(\sigma)=140 \end{gathered}`

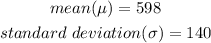
STEP 3: Solve the question

In this problem, we have that:

`\begin{gathered} 318=598-280=598-2(\sigma)=\mu-2\sigma \\ 878=598+280=598+2\sigma=\mu+2\sigma \end{gathered}`

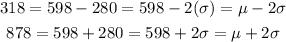
So 318 is 2 standard deviations below the mean.

So 878 is 2 standard deviations above the mean.

The EMPIRICAL RULE (or the 68-95-99.7 Rule) says that about 68% of the data is between 1 standard deviation below the mean and 1 standard deviation above the mean. Below the shaded part is about 68% of the area between the normal curve and the z-axis.

The EMPIRICAL RULE (or the 68-95-99.7 Rule) also says that about 95% of the data is between 2 standard deviations below the mean and 2 standard deviations above the mean. Below the shaded part is about 95% of the area between the normal curve and the z-axis.

Going by this descriptions above, this means that:

The percentage of people taking the test who score between 318 and 878 is 95%