We can calculate the shaded area as the area of the trapezoid less the area of the circle.
The area of the trapezoid is:
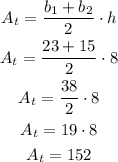
The area of the circle of radius r=8/2=4 ft is:
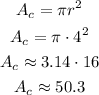
Then, the shaded area is the difference between the area of the trapezoid and the area of the circle:
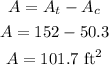
Answer: 101.7 ft^2