Answer:

Step-by-step explanation:
Here, we want to write an equation for the graph shown
The graph of x^2 is an upward-facing graph
The graph we have shown below is a graph that has been reflected and shifted
To get the equation of the graph we need to write it in the vertex form
The vertex form is:
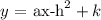
The vertex of the graph is at (h,k)
Looking at the given graph, we have the vertex at (-1,1)
Thus, we have the equation as:
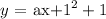
Lastly, we need to get the value of a
We can use the point (1,0)
Substituting this value:

Thus, we have the equation of the plotted graph as:
