Given data:
The tensile strength of the string is,
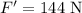
The mass of the car is,
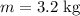
The length of the string is,
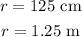
The force acting on the car is,
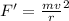
where a is the linear acceleration and m is the mass of the car.
Substituting the known values,
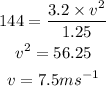
Thus, the angular speed of the car is,
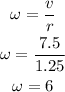
Each distance of each revolution is,
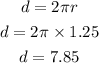
Thus, the value of angular speed in terms of revolution is,

Thus, the maximum angular speed of the toy car is 45.6 revolutions per minute.