Answer:
Step-by-step explanation:
Given:
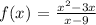
To find:
the graph that represents the function f
To determine the graph, we need to check if the expression can be simplified:

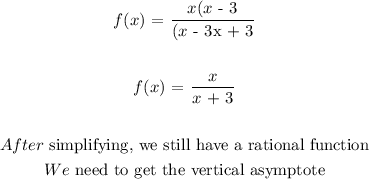
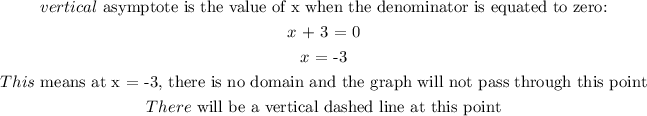
We will check the options for the graph that satisfies the above:
Only option B has a vertical dased line at x = -3. Also the graph doesn't pass t