Question

Pls help I have a final on this number 1

Answer 1

1a)

*A reflection across the x-axis

*A vertical compression

*A horizontal translation 3 units left

*A vertical translation up 5 units

1b)

*A reflection across the x-axis

*A vertical stretch

*A horizontal translation 2 units right

*A vertical translation down 11 units

Step-by-step explanation:

Given:

`\begin{gathered} f(x)=-(1)/(2)(x+3)^2+5 \\ h(x)=-3(x-2)^2-11 \end{gathered}`

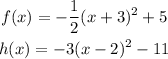
To:

Describe the transformation effects from the parent graph g(x) = x^2

Recall that a quadratic function in vertex form;

`f(x)=a(x-h)^2+k`

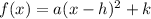
where;

a > 1 represents a vertical stretch

0 < a < 1 represents a vertical compression

-h represents horizontal translation right h units

+h represents horizontal translation left h units

k represents vertical translation up k units

-k represents vertical translation down k units

-a represents a reflection across the x-axis

1(a) Comparing the below-given function with the vertex function, the transformations are as listed below;

`f(x)=-(1)/(2)(x+3)^2+5`

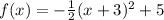
*A reflection across the x-axis

*A vertical compression

*A horizontal translation 3 units left

*A vertical translation up 5 units

1(b) Comparing the below-given function with the vertex function, the transformations are as listed below;

`h(x)=-3(x-2)^(2)-11`

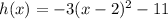
*A reflection across the x-axis

*A vertical stretch

*A horizontal translation 2 units right

*A vertical translation down 11 units