ANSWER:
1a)
*A reflection across the x-axis
*A vertical compression
*A horizontal translation 3 units left
*A vertical translation up 5 units
1b)
*A reflection across the x-axis
*A vertical stretch
*A horizontal translation 2 units right
*A vertical translation down 11 units
Step-by-step explanation:
Given:

To:
Describe the transformation effects from the parent graph g(x) = x^2
Recall that a quadratic function in vertex form;

where;
a > 1 represents a vertical stretch
0 < a < 1 represents a vertical compression
-h represents horizontal translation right h units
+h represents horizontal translation left h units
k represents vertical translation up k units
-k represents vertical translation down k units
-a represents a reflection across the x-axis
1(a) Comparing the below-given function with the vertex function, the transformations are as listed below;
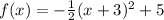
*A reflection across the x-axis
*A vertical compression
*A horizontal translation 3 units left
*A vertical translation up 5 units
1(b) Comparing the below-given function with the vertex function, the transformations are as listed below;
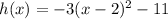
*A reflection across the x-axis
*A vertical stretch
*A horizontal translation 2 units right
*A vertical translation down 11 units