Plot two points on the graph of the function, and also draw the asymptote.

Question

asked Jan 17, 2023 41.2k views

1 Answer

Aatrujillob · Answer 1 · 2023-01-22T20:53:09+0000

SOLUTION

Write out the function given.

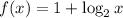
$f(x)=1+\log _2x$

To plot two point in the function, let obtain the point in from the function.

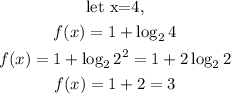
$\begin{gathered} \text{let x=4,} \\ f(x)=1+\log _24 \\ f(x)=1+\log _22^2=1+2\log _22 \\ f(x)=1+2=3 \\ \end{gathered}$

Then, the first point is

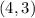
Similarly, let x=2

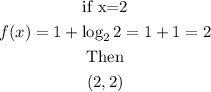
$\begin{gathered} \text{if x=2} \\ f(x)=1+\log _22=1+1=2 \\ \text{Then} \\ (2,2) \end{gathered}$

Then the point is

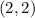
The two point to use are

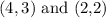
$(4,3)\text{ and (2,2)}$

The point are (2,2) and (4,3)

Then the vertical asymptotes is obtain by equating the logatithm expression to zero

Hence

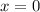
Vertical asymptotes is x=0

Hence

The image of the graph is given below