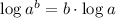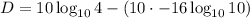Question

The decibel rating D is related to the sound intensity I by the formula D=10log(I/(10^-16)) for the noise in decibels. a) let D and d represent the decibel ratings of sounds of intensity I and i, respectively. Using properties of logarithms, find a simplified formula for the difference between the two ratings, D-d, in terms of the two intensities I and i. b) If a sounds intensity quadruples, how many decibels louder does the sound become?

Answer 1

The decibel D is related by the formula:

`D=10\log _(10)((l)/(10^(-16)))`

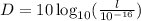
Now, let's find a simplified formula between the two rating D and I using properties of logarithms:

We are going to use the same formula but changing D by d and I by i, then subtract both formulas:

`d=10\log _(10)((i)/(10^(-16)))`

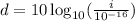
D-d:

`D-d=10\log _(10)((I)/(10^(-16)))\text{ - 10}\log _(10)((i)/(10^(-16)))`

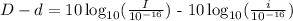
Factorize the number 10:

`D-d=10\lbrack\log _(10)((I)/(10^(-16)))-\log _(10)((i)/(10^(-16)))\rbrack`

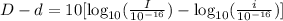
Use the next rule of logarithms:

`\log _a((m)/(n))=\log _am-\log _an`

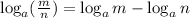
So:

`D-d=10\lbrack\log _(10)I-\log _(10)10^(-16)-\log _(10)i+\log _(10)10^(-16)\rbrack`

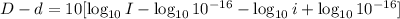
Operate the common terms:

`D-d=10\lbrack\log _(10)I-\log _(10)i\rbrack`

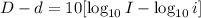
Now, we are going to use the same rule presented before by changing the rest by a division:

`D-d=10\log _(10)((I)/(i))`

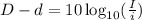
With the before formula you can solve the difference between two ratings.

b)The sound intensity now quadruples, using the first given formula find the decibels louder:

So I = 4, replace this value and solve:

`D=10\log _(10)((4)/(10^(-16)))`

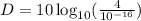
We use the same property changing the division by a subtraction:

`D=10\log _(10)4-10\log _(10)10^(-16)`

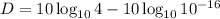
Now, we are going to use the next property:

`\log _{}a^b=b\cdot\log _{}a`
`D=10\log _(10)4-(10\cdot-16\log _(10)10)`