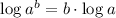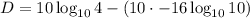The decibel D is related by the formula:
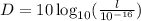
Now, let's find a simplified formula between the two rating D and I using properties of logarithms:
We are going to use the same formula but changing D by d and I by i, then subtract both formulas:
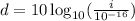
D-d:
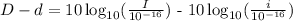
Factorize the number 10:
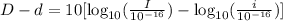
Use the next rule of logarithms:
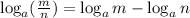
So:
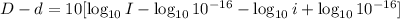
Operate the common terms:
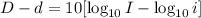
Now, we are going to use the same rule presented before by changing the rest by a division:
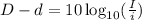
With the before formula you can solve the difference between two ratings.
b)The sound intensity now quadruples, using the first given formula find the decibels louder:
So I = 4, replace this value and solve:
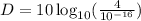
We use the same property changing the division by a subtraction:
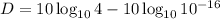
Now, we are going to use the next property: