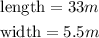Question

The shore, a rope, and a dock that is 8 meters long enclose a rectangular swimming area along thelakeshore. The length of swimming area is 6 meters more than its width and the swimming area must bemore than 180 square meters. If the rope is 34 meters long, then what are the dimensions of theswimming area?

Answer 1

So we have two conditions, the first one is that the length (L) of the swimming area is 6 meters more than the width (W) so:

`L=6W`

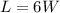
and the other condition is that the area is 180 square meters so we can writte it like:

`180=L\cdot W`

Now we have 2 equations and 2 ingognitas so we can replace the first equation into the second equation like this:

`180=(6W)\cdot W`

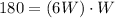
and we solve for W so

`\begin{gathered} 180=6W^2^{} \\ W^2=(180)/(6)=30 \\ W=\sqrt[]{30}=5.5 \end{gathered}`

Now with the value of W we can replace it in the first equation so:

`L=6(5.5)`

so:

`L=33`

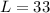
The dimensions are:

`\begin{gathered} \text{length}=33m \\ \text{width}=5.5m \end{gathered}`