Given data:
The mass of the ball is m=0.25 kg.
The spring constant is k=100 N/m.
The speed of the ball is v=6.8 m/s.
The amount of energy stored in the spring in the form of elastic potential energy will equal to the kinetic energy of the ball. It can be applied as,
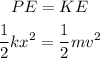
Here, x is the compression in the spring.
Substitute the given values in above equation,
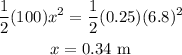
Thus, the initial compression of the spring is 0.34 m.