Answer:
Explanation :
GIVEN THE EQUATION :

(i) Find the derivative of cos^2 (x)
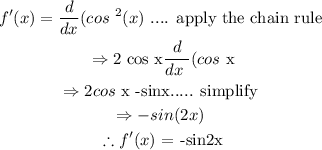
(ii) Now that we have calculated the derivative of cos^2 (x) = -sin(2x)
at x = /6 :
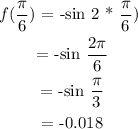
This means that our point is ( /6 ;- 0.018)
(iii) Calculate the slope of the tangent line :
m = f'( /6 )
= -sin2