Question

Given f(x) = cos^2 (x), find the equation of the tangent line at x = π/6

Answer 1

Answer:

Explanation :

GIVEN THE EQUATION :

`f(x)\text{ = cos }^2(x)\text{ }`

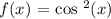
(i) Find the derivative of cos^2 (x)

`\begin{gathered} f^(\prime)(x)=(d)/(dx)(cos\text{ }^2(x)\text{ \rparen.... apply the chain rule } \\ \Rightarrow2\text{ cos \lparen x\rparen }\frac{d}{dx\text{ }}(cos\text{ \lparen x\rparen\rparen} \\ \Rightarrow2cos\text{ x \lparen-sinx\rparen ..... simplify } \\ \Rightarrow-sin(2x)\text{ } \\ \therefore f^(\prime)(x)\text{ = -sin\lparen2x\rparen } \\ \\ \end{gathered}`

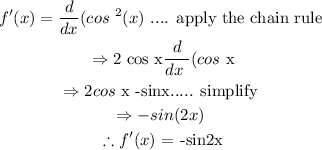
(ii) Now that we have calculated the derivative of cos^2 (x) = -sin(2x)

at x = /6 :

`\begin{gathered} f((\pi)/(6))\text{ = -sin \lparen2 * }(\pi)/(6)) \\ \text{ = -sin }(2\pi)/(6) \\ \text{ = -sin }(\pi)/(3) \\ \text{ = -0.018} \end{gathered}`

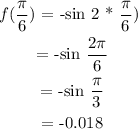
This means that our point is ( /6 ;- 0.018)

(iii) Calculate the slope of the tangent line :

m = f'( /6 )

= -sin2