Question

6. (5 points) Using the method of Bragg’s law, can you use 5 x-rays to measure the spacing between atoms in a crystal if those atoms are spaced 0.250 apart? (You must show the work you used to determine if it was possible.)

Answer 1

The energy of the X-ray is,

`E=5\text{ keV=5}*10^3*1.6*10^(-19)J`

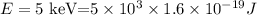
the wavelength of the X-ray is then,

`l=(hc)/(E)`

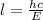
Here,

`h=6.62*10^(-34)J\text{ }`
`c=3*10^8\text{ m/s}`

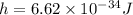
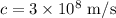
substituting the values we get the wavelength,

`\begin{gathered} l=(6.62*10^(-34)*3*10^8)/(5*10^3*1.6*10^(-19)) \\ =0.248*10^(-9)\text{ m} \\ =0.248\text{ nm} \end{gathered}`

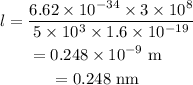
we can see here the given atomic space is nearly equal to the order of the calculated wavelength

for the Bragg's law experiment this is the main condition that the atomic spacing should be of the order of the wavelength of the light

Hence the given X-ray can be used for the purpose.