1. Solve A PQR. When working with triangles, the term 'solve' means to find all of the unknown sides and angles in the triangle. 25 cm 24 cm R

Question

asked Jul 21, 2023 228k views

1 Answer

Fygo · Answer 1 · 2023-07-25T14:25:41+0000

This is a right triangle.

To find length PQ we need to use the pythagorean theorem; we have to remember that it states that:

where a and b are the legs and c is the hypotenuse.

Applying it to the triangle given we have:

$\begin{gathered} 25^2=PQ^2+24^2 \\ PQ^2=25^2-24^2 \\ PQ^2=625-576 \\ PQ^2=49 \\ PQ=\sqrt[]{49} \\ PQ=7 \end{gathered}$

Therefore the side PQ=7

To determine the angle R we can use the cosine function that is defined as:

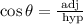
$\cos \theta=\frac{\text{adj}}{\text{ hyp}}$

then for angle R we have:

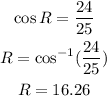
$\begin{gathered} \cos R=(24)/(25) \\ R=\cos ^(-1)((24)/(25)) \\ R=16.26 \end{gathered}$

Hence angle R=16.26°.

Now, for angle P we use the fact that the interior angles of any triangle have to add to 180°, then we have:

$\begin{gathered} P+R+Q=180 \\ P+16.26+90=180 \\ P=180-90-16.26 \\ P=73.74 \end{gathered}$

Therefore angle P=73.74°