This is a right triangle.
To find length PQ we need to use the pythagorean theorem; we have to remember that it states that:
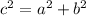
where a and b are the legs and c is the hypotenuse.
Applying it to the triangle given we have:
![\begin{gathered} 25^2=PQ^2+24^2 \\ PQ^2=25^2-24^2 \\ PQ^2=625-576 \\ PQ^2=49 \\ PQ=\sqrt[]{49} \\ PQ=7 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/sh5qbqkhta3acv9uhjf046y09tm1umtdaj.png)
Therefore the side PQ=7
To determine the angle R we can use the cosine function that is defined as:
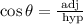
then for angle R we have:
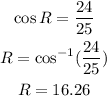
Hence angle R=16.26°.
Now, for angle P we use the fact that the interior angles of any triangle have to add to 180°, then we have:
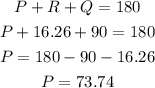
Therefore angle P=73.74°