We have here two equations that we need to determine in order to solve the question.
First, we have:
1. If you pay $80 for a monthly pass and then you pay $5 for each visit.
2. You can pay $15 for each visit with no monthly pass.
In the first case, the expression that translates that in an equation is:
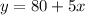
In the second case, the expression is:
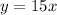
Since y is the total cost to go to the gym, and we need to know what the cost is when either option cost the same, we can equate both equations as follows:
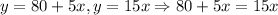
Then, we need to solve the last equation subtracting 5x to both side of it:
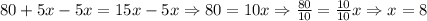
Thus, the value for x is 8. To find the value of the cost, we can substitute this value in either equation. The cost will be the same:
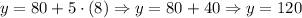
Or
![undefined]()