Question

At a local gym you can either pay $80 for a monthly pass and then pay $5 for each visit or you can pay $15 for each visit with no monthly pass what is the cost when at the point when either option cost the same

Answer 1

We have here two equations that we need to determine in order to solve the question.

First, we have:

1. If you pay $80 for a monthly pass and then you pay $5 for each visit.

2. You can pay $15 for each visit with no monthly pass.

In the first case, the expression that translates that in an equation is:

`y=80+5x`

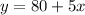
In the second case, the expression is:

`y=15x`

Since y is the total cost to go to the gym, and we need to know what the cost is when either option cost the same, we can equate both equations as follows:

`y=80+5x,y=15x\Rightarrow80+5x=15x`

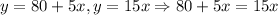
Then, we need to solve the last equation subtracting 5x to both side of it:

`80+5x-5x=15x-5x\Rightarrow80=10x\Rightarrow(80)/(10)=(10)/(10)x\Rightarrow x=8`

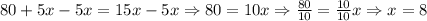
Thus, the value for x is 8. To find the value of the cost, we can substitute this value in either equation. The cost will be the same:

`y=80+5\cdot(8)\Rightarrow y=80_{}+40\Rightarrow y=120`

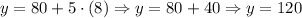
Or