Question

Put the quadratic into vertex form and state the coordinates of the vertexy=x2+6x+13

Answer 1

Quadratic function: Vertex form is represented by:

`\begin{gathered} f(x)=a(x-h)^2+k \\ \text{where (h, k) is the vertex} \end{gathered}`

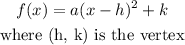
Standard form is:

`\begin{gathered} f(x)=ax^2+bx+c \\ y=x^2+6x+13 \end{gathered}`

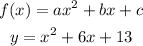
To get the vertex of the quadratic graph, we can use the following formulas:

`\begin{gathered} h=-(b)/(2a) \\ k=f(h) \end{gathered}`

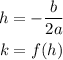
Then, calculating h:

`\begin{gathered} h=-(6)/(2(1)) \\ h=-(6)/(2)=-3 \end{gathered}`

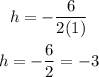
k, would be f(-3):

`\begin{gathered} k=(-3)^2+6(-3)+13 \\ k=9-18+13 \\ k=4 \end{gathered}`

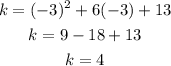
Therefore, the quadratic function in vertex form would be:

`y=(x+3)^2+4`

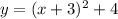
Coordinates of the vertex (-3, 4).