Quadratic function: Vertex form is represented by:
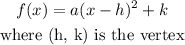
Standard form is:
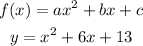
To get the vertex of the quadratic graph, we can use the following formulas:
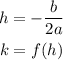
Then, calculating h:
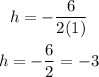
k, would be f(-3):
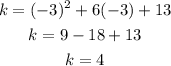
Therefore, the quadratic function in vertex form would be:
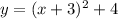
Coordinates of the vertex (-3, 4).