Given the functions

1) Notice that both functions are exponential. In general, an exponential growth function can be written as shown below
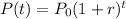
where r is the rate of growth of function P(t).
Therefore, in our case,
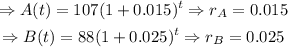
Thus, forest B is growing at a faster rate than forest A. The answer to part 1 is forest B
2) and 3) The amount of trees in each forest is given by A(0) and B(0), respectively; thus,
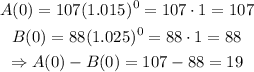
Therefore, forest A had a greater number of trees initially, and it exceeded forest B by 19 trees. The answer to part 2 is Forest A, and the answer to part 3 is 19 trees.
4) and 5)
Similarly, we need to find the values of A(30) and B(30)

Therefore, the answer to part 4 is Forest B, and the answer to part 5 is 17.34 trees.