Question

For the following exercises consider the scenario..Drop down options for 1 2 4 are Forest A or Forest B

Answer 1

Given the functions

`\begin{gathered} A(t)=107(1.015)^t \\ \text{and} \\ B(t)=88(1.025)^t \end{gathered}`

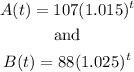
1) Notice that both functions are exponential. In general, an exponential growth function can be written as shown below

`P(t)=P_0(1+r)^t^{}`

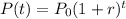
where r is the rate of growth of function P(t).

Therefore, in our case,

`\begin{gathered} \Rightarrow A(t)=107(1+0.015)^t\Rightarrow r_A=0.015 \\ \Rightarrow B(t)=88(1+0.025)^t\Rightarrow r_B=0.025 \end{gathered}`

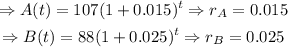
Thus, forest B is growing at a faster rate than forest A. The answer to part 1 is forest B

2) and 3) The amount of trees in each forest is given by A(0) and B(0), respectively; thus,

`\begin{gathered} A(0)=107(1.015^{})^0=107\cdot1=107 \\ B(0)=88(1.025)^0=88\cdot1=88 \\ \Rightarrow A(0)-B(0)=107-88=19 \end{gathered}`

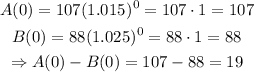
Therefore, forest A had a greater number of trees initially, and it exceeded forest B by 19 trees. The answer to part 2 is Forest A, and the answer to part 3 is 19 trees.

4) and 5)

Similarly, we need to find the values of A(30) and B(30)

`\begin{gathered} A(30)=107(1.015)^(30)=167.24958\ldots \\ B(30)=88(1.025)^(30)=184.58594\ldots \\ \Rightarrow B(30)-A(30)\approx17.34 \end{gathered}`

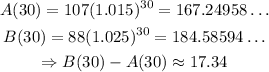
Therefore, the answer to part 4 is Forest B, and the answer to part 5 is 17.34 trees.