Question

my question is:the sequence(1,4),(2,8),(3,16),(4,32)i need to solve for the next one using recursive formulafor station 5Theres 3 parts: part a: is it arithmetic sequence or geometric part b: use recursive formula to determine the time she will complete station 5 show your work and part c: use explicit formula to find the time she will complete station 8those are the full questionsim on part b and c, thats what i need help with

Answer 1

So the ordered pairs given tell us how much time has passed since the beginning at each station. If we analyze this data as a sequence we have that the terms of the sequence are given by the time and their orders are given by the station number. Then the terms of the sequence are:

`4,8,16,32\ldots`

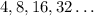
As you can see the difference between consecutive terms is not always the same. This means that this is not an arithmetic sequence. So this is probably a geometric sequence. The general formula for such type of sequence is:

`a_n=a_1\cdot r^(n-1)`

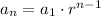
Where the n denotes the term order, a₁ is the first term (in this case it's 4) and r is known as the common ratio. So we know that the first term is 4 so we get:

`a_n=4\cdot r^(n-1)`

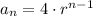
We can use the other terms of the sequence to find r:

`\begin{gathered} 8=a_2=4\cdot r^(2-1)=4\cdot r \\ 8=4r \end{gathered}`

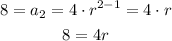
If we divide both sides of this equation by 4 we get the value of r:

`\begin{gathered} (8)/(4)=(4r)/(4) \\ 2=r \end{gathered}`

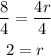
So r=2 and the general formula looks like this:

`a_n=4\cdot2^(n-1)`

If we take n=3 and n=4 we should get 16 and 32. Let's check this:

`\begin{gathered} a_3=4\cdot2^(3-1)=4\cdot4=16 \\ a_4=4\cdot2^(4-1)=4\cdot8=32 \end{gathered}`

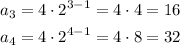
So r is in deed equal to 2. Then the answer to part A is that this is a geometric sequence.

In part B we have to find the term for n=5. However we have to use a recursive formula and the one I just found is explicit. A recursive formula gives you the value of a term using the value of a previous term. Now let's see the differences between consecutive terms:

`\begin{gathered} a_2-a_1=8-4=4=2^2 \\ a_3-a_2=16-8=8=2^3 \\ a_4-a_3=32-16=16=2^4 \end{gathered}`

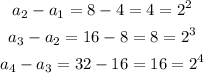
So we have that the difference between consecutive terms is given by:

`a_n-a_(n-1)=2^n`

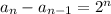
Then the recursive formula we have to use is given by this expression:

`a_n=a_(n-1)+2^n`

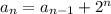
Then the time when Aurora completes station 5 is given by:

`a_5=a_(5-1)+2^5=a_4+32=32+32=64`

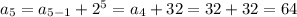
Then the answer to part B is 64 minutes.

For part C we just need to use the explicit formula we found in part A:

`a_n=4\cdot2^(n-1)`

We have to take n=8:

`a_8=4\cdot2^(8-1)=4\cdot2^7=4\cdot128=512`

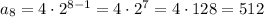
Then the answer to part C is 512 minutes.