Step-by-step explanation:
We are told to find the scale factor and the translation of the triangle ABC
To obtain the answer, we can follow the steps below
Step 1:
Get the dimensions of the triangle ABC and compare with triangle DEF
For ABC, the dimensions in units are
The dimensions of DEF are
We can compare similar sides to get the scale factor
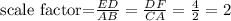
Therefore, the scale factor is 2
The triangle was reflected across the x-axis, and
moved through the translation by 2 units