Question

A canoe rental service charges per hour. The price canbe represented by the following relationship:P(h) = 8.5h + 30Let P^-1 be the inverse function of P.a) Write a statement that describes P^-1(x)b) Find an equation for P^-1(x)c) Determine P^-1 (72.5)

Answer 1

Let's look for the possible statement that describes the inverse of the function P(h). If we are looking for the P(h) as the function for canoe rental as charge per hour, the inverse will be the reverse of it, hence, we are dealing with hours per charge. Therefore,

a) P^-1(x) describes the canoe rental service by hours per charge.

b) To solve the inverse of the function, the first step is to change P(x) with y, we have

`y=8.5h+30`

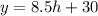
Then, replace all y's with h and h's with y's, we now have

`h=8.5y+30`

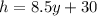
Solve for y, we get

`\begin{gathered} h-30=8.5y \\ (8.5y)/(8.5)=(h-30)/(8.5) \\ y=(h-30)/(8.5) \end{gathered}`

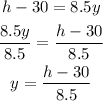
Finally, replace y with P^-1(h).

`P^(-1)(h)=(h-30)/(8.5)`

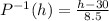
Or, if we want it to write in terms of P^-1(x), change h's to x's, having

`P^(-1)(x)=(x-30)/(8.5)`

where the equation above describes the inverse of the function P(h).

c) To solve for P^-1(72.5), just simply substitute x to 72.5 and solve. We have

`P^(-1)(72.5)=(72.5-30)/(8.5)=5`

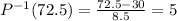
Hence, P^-1(72.5) is equal to 5.