Question

Three identical 6.39 x 10-4 Ccharges are on the corners ofan equilateral triangle of side3.35 m. Find the magnitude ofthe net force on 93.9291(Make sure you know the direction of each force!Remember, equilateral triangles have 60 degree interiorangles.)93

Answer 1

Given:

• Number of identical charges = 3

,

• Charge, q1 = q2 = q3 = 6.39 x 10⁻⁴ C.

,

• Length of each side of the triangle, d = 3.35 m

,

• θ = 60 degrees

Let's find the magnitude of the net force on q3.

For forces acting on q3 due to q1 and q2, apply the formula:

`\begin{gathered} F=(kq_1q_2)/(d^2) \\ \\ F=(9*10^9*(6.39*10^(-4))*(6.39*10^(-4)))/(3.35^2) \\ \\ F=(3674.889)/(11.2225) \\ \\ F=327.46\text{ N} \end{gathered}`

The magnitude of net force on all 3 charges will also be equal.

Now, to find the magnitude of the net force acting on q3, apply the formula:

`\begin{gathered} F_(net)=√(F^2+F^2+2F^2cos\theta) \\ \\ F_(net)=√(2F^2+2F^2cos\theta) \end{gathered}`

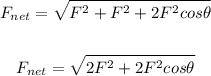
Thus, we have:

`\begin{gathered} F_(net)=√(2(327.46)^2+2(327.46)^2cos60) \\ \\ F_(net)=√(214460.1032+214460.1032(0.5)) \\ \\ F_(net)=√(214460.1032+107230.0516) \\ \\ F_(net)=√(321690.1548) \\ \\ F_(net)=567.18\text{ N} \end{gathered}`

Therefore, the magnitude of net force acting on charge 3 is 567.18 N.

• ANSWER:

567.18 N