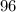Question:
Solution:
Applying the Pythagorean theorem, we obtain:
![b=\sqrt[\square]{20^2-12^2}](https://img.qammunity.org/2023/formulas/mathematics/college/uf025yw8a3wl84s0qjxo890t6moc8yh6f6.png)
this is equivalent to:
![b=\sqrt[\square]{400^{}-144^{}}=16](https://img.qammunity.org/2023/formulas/mathematics/college/mqsay1wcueb3im1oxb8lyes2oucr5eq25b.png)
so that, we can conclude that the lenght of the base is:
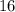
now, the area A of a triangle with base b and height h is given by the following equation:
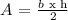
note that in this case b= 16 and h=12, then the area of the given triangle is:
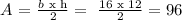
so that, we can conclude that the area of the triangle is: