1. Colinear points are the ones that are in the same line.
In this example, K is colinear to J and L (referring to line a).
It can be N and M, referring to line c.
2. As the line has the points H and K included, it can be named HK.
3. The intersection of a line and a plane, assuming that the line is not included in the plane, is a point. In this case, the intersection of line c and plane R is point K.
4. A point is coplanar to a plane or another point when it belongs to the plane.
In this case the point M is not coplanar to the plane R (it is outside of the plane).
5. Each face of the prism is a plane and it is can be defined by 3 points. So in this case we have 5 planes (four faces and one base, that is W).
6. We can assign a name for a plane with 3 points that belong to that plane. A possible name is ABC.
7. The intersection of plane W and ADE is the line that goes through the points A and D. We can call this line with the name AD.
8. E, C or D are no colinear to A and B. They do not belong to the line that goes through the points A and B (or the line AB).
9. DF is the sum of DE and EF, so we have:
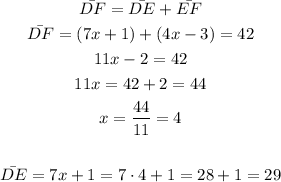
DE = 29
10. We know that:

11. If S is the midpoint of RT, then RS=ST.
We would have:

12. If y bisects AC, then AB=BC. Then we have:
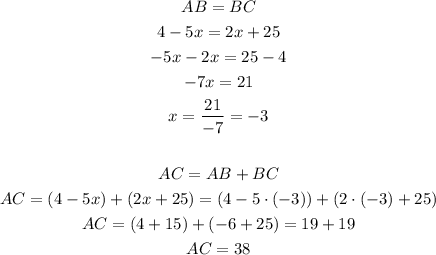
13. AB is half the value of AC, so we have:
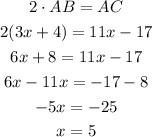
Then, we can calculate CD = AC

We can define DE as DE = CE - CD. We can calculate it as:
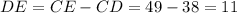
DE = 11