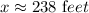Let x be the height of the building
We will first make a sketch
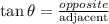
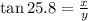

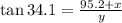
substitute the y-value in the above
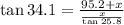
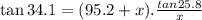
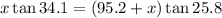
x (0.677) = (95.2 + x)0.4834
open the parenthesis
0.677x = 46.01968 + 0.4834x
subtract 0.4834x from both-side of the equation
0.677x - 0.4834x = 46.01968
0.1936x = 46.01968
Divide both-side by 0.1936
x≈ 237.7 ft