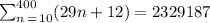We know that the sum of the first n terms of an arithmetic sequence is given by:
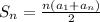
Now this formula does not apply to our case since we are not starting at the first term of the summation. But we know that:
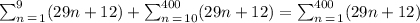
then:
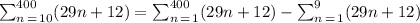
And we can apply the first formula for both sums at the right of the last equation since they start at the first term of the sum.
In this case we have that:
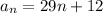
and that:
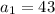
We also have that:
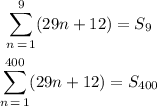
Then we have:
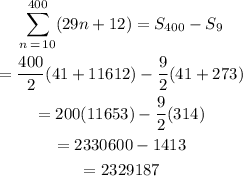
Therefore: