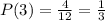EXPLANATION
The probability for 1 , 2 and 3 are not equally likely because the fill different dimensions on the spinner.
The equation for the probability is as follows:
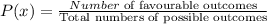
We need to divide the spinner in same divided parts:
#1 Parts: 3
#2 Parts: 5
#3 Parts: 4
Number of total parts = 12
The possible outcome for number 1 is:
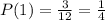
The possible outcome for #2 is as follows:
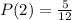
The possible outcome for #3 is as shown as follows: