Question

I need to use the buying binomial distribution formulaI need to find A)Probability 4successesB) Probability 2 successesC) Probability at most 3 successes( HINT When you are finding P( at most 3 successes you need = P(x ≤3)= P(x= 0) + P(x = 1)+ P(x = 2)+ P(x = 3)You need to solve each one individually with the binomial distribution formula then add sum of x=0 + sum of x=1+ sum x=2 + x=0PLEASE HELP ME With EXERCISE ASAP GED PRACTICE Please look at picture for exercise

Answer 1

Given:

There are number of trials and possibility of success

Required:

We need to find the probability by binomial distribution formula

Step-by-step explanation:

A)

n=15

p=0.4

q=0.6

x=4

Substitute the values in the formula

`P(4)=(15!)/(11!4!)(0.4)^4(0.6)^(11)=0.12`

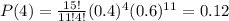
B)

n=12

p=0.2

q=0.8

x=2

Substitute the values in the formula

`P(2)=(12!)/(10!2!)(0.2)^2(0.8)^(10)=0.28`

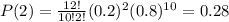
C)

n=20

p=0.05

q=0.95

x=0,1,2,3

Substitute the values in the formula

`\begin{gathered} P(0)=(20!)/(20!0!)(0.05)^0(0.95)^(20)=0.35848 \\ \\ P(1)=(20!)/(19!1!)(0.05)^1(0.95)^(19)=0.37735 \\ \\ P(2)=(20!)/(18!2!)(0.05)^2(0.95)^(18)=0.18867 \\ \\ P(3)=(20!)/(17!3!)(0.05)^3(0.95)^(17)=0.0.05958 \end{gathered}`

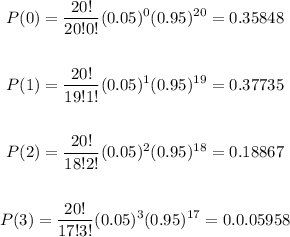
Now add all

`P(atmost\text{ 3\rparen}=0.98408`

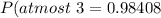
Final answer:

A) 0.12

B) 0.28

C) 0.98408