Given:
There are number of trials and possibility of success
Required:
We need to find the probability by binomial distribution formula
Step-by-step explanation:
A)
n=15
p=0.4
q=0.6
x=4
Substitute the values in the formula
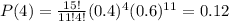
B)
n=12
p=0.2
q=0.8
x=2
Substitute the values in the formula
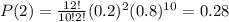
C)
n=20
p=0.05
q=0.95
x=0,1,2,3
Substitute the values in the formula
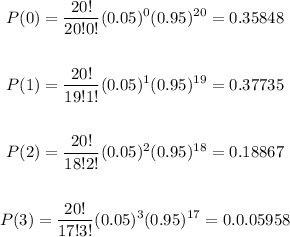
Now add all
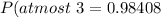
Final answer:
A) 0.12
B) 0.28
C) 0.98408