The expression we have is:
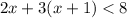
Step 1. Use distributive property to multiply 3 by x and by 1:
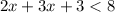
Step 2. Combine variable like terms 2x + 3x which results in 5x:
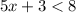
Step 3. Substract 3 from both sides of the inequation:
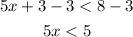
Step 4. Divide both sides by 5:
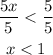
Solution: x < 1
Step 5. Graph the solution
The solution is represented by the red line on the graph, which includes all of the values less than 1, (not including 1 becuase we have < and not ≤ ).