Question

graph the line with the given slope and point Its one question with 3 partsI previously removed the letter because it was written in Chinese

Answer 1

We are given the slope and one point of a line. To graph the line, let's remember the general form for a line equation, that is:

`y=mx+b`

Where "m" is the slope and "b" the y-intercept. Replacing the value of the slope, we get:

`y=-3x+b`

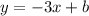
Now, to determine the value of "b" we replace the known point (1,-2), knowin that when x = 1, y = -2.

`-2=-3(1)+b`

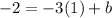
Solving the operations:

`-2=-3+b`

Now we add 3 on both sides:

`\begin{gathered} -2+3=-3+3+b \\ 1=b \end{gathered}`

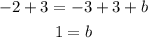
Replacing in the equation for the line:

`y=-3x+1`

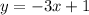
To graph this equation we need to know two points through which the line passes. We can determine those points by inserting values of "x" into the equation and solving to get the value of "y". Replacing x = 0, we get:

`\begin{gathered} y=-3(0)+1 \\ y=1 \end{gathered}`

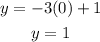
Repalcing x = 1, we get:

`\begin{gathered} y=-3(1)+1 \\ y=-3+1=-2 \end{gathered}`

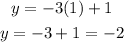
Therefore, the line passes through the points (0,1) and (1,-2). We plot those points and join them with a line, like this: