Question

The graph shows the function f(x). Which value is closest to the average rate of change from x = 1 to x = 4? A. −3.5B. −2.3C. −1.4D. −0.3A parabola is graphed on a coordinate plane. The horizontal x-axis ranges from negative 1 to 10 in increments of 1. The vertical y-axis ranges from negative 5 to 10 in increments of 1. The vertex is located at begin ordered pair 3.375 comma negative 4.188 end ordered pair. The parabola opens upward. It passes through the horizontal axis at begin ordered pair 1.603 comma 0 end ordered pair and begin ordered pair 5.147 comma 0 end ordered pair.

Answer 1

B. ​−2.3

Explanation:

The average rate of change of f(x) from x = 1 to x = 4 is calculated using the formula below:

`Rate\;of\;Change=(f(4)-f(1))/(4-1)`

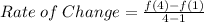
From the graph:

• When x=4, the value of f(x)=-4 i.e. f(4)=-4

,

• When x=1, the value of f(x)=3 i.e. f(1)=3

Therefore, the rate of change is:

`Rate=(-4-3)/(3)=-(7)/(3)=-2.33`

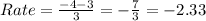
Therefore, the value that is closest to the average rate of change is -2.3.

Option B is correct.