Question

Its all in one photo so it can be easier to understand !!!

Answer 1

Both functions start up at the same y value when x = 0:

`\begin{gathered} f(0)=50((1)/(2))^0=50\cdot1=50 \\ g(0)=50((1)/(3))^0=50\cdot1=50 \end{gathered}`

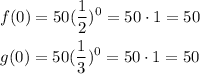
However, from there we will multiply by the exponential term.

Since the numbers 2 and 3 are on the denominator, they work on contrary, because when we divide by a higher number, we get a smaller result.

So, for x = 1, for example, since 3 > 2 and there are on the denominato, g(1) wil be less than f(1):

`\begin{gathered} f(1)=50((1)/(2))^1=50\cdot(1)/(2)=25 \\ g(1)=50((1)/(3))^1=50\cdot(1)/(3)=16.66\ldots \end{gathered}`

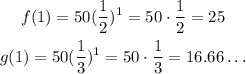
So, We start by noticing that 3 > 2, but since they are on the denominator, the conclusion is the other way around: graph f lies above the graph g, so graph f is the graph 1 and graph g is the graph 2.