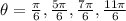a)
The given equation is
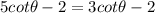
Subtract 3cot(theta) from each side
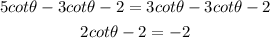
Add 2 to both sides
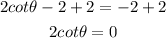
Divide both sides by 2
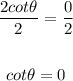
cot(theta) = 0 at theta = pi and theta = 3/2pi
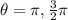
b)
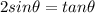
Change tan(theta) to sin(theta)/cos(theta)
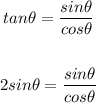
Multiply both sides by cos(theta)
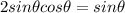
Subtract sin(theta) from both sides
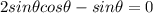
Take sin(theta) as a common factor on the left side
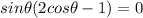
Equate each factor by 0
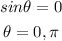
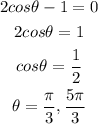
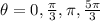
c)
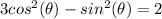
Change sin^2(theta) to 1 - cos^2(theta)
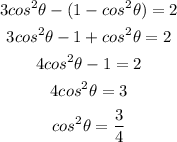
Take a square root for each side
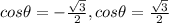
The values of theta are