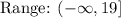Answer:
Domain:
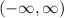
Range:
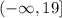
Step-by-step explanation:
Given the below quadratic function in vertex form;
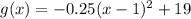
The domain of a function is the set of all possible input values for which a function is real and defined.
Looking at the given function, we can see that the function doesn't have radicals so it won't result in an imaginary solution and that is not a fraction so we won't have an undefined solution, therefore the domain of the function is all x values which can be written in interval notation as;
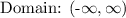
A quadratic equation in vertex is generally given as;
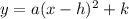
where (h, k) is the coordinate of the vertex.
Note that when;
a > 0, the range is all real numbers greater than or equal to k
a < 0, the range is all real numbers less than or equal to k
Comparing both functions, we can see that a = -0.25 and k = 19.
We can see that a < 0, therefore the range of the given function is all real numbers less than or equal to 19, written in interval notation as;