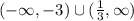Question

Solve: | 3x+4 | +5>10

Answer 1

`|3x+4|+5>10`

To solve for x in the above equation, here are the steps:

1. Subtract 5 on both sides of the equation.

`\begin{gathered} |3x+4|+5-5>10-5 \\ |3x+4|>5 \end{gathered}`

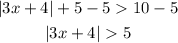
2. Extract the two possible results of an absolute value.

`\begin{gathered} -(3x+4)>5 \\ +(3x+4)>5 \end{gathered}`

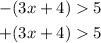
3. Solve the x value in each equation.

`\begin{gathered} -(3x+4)>5 \\ -3x-4>5 \\ \text{Add 4 on both sides.} \\ -3x>9 \\ \text{Divide -3 on both sides. } \\ x<-3 \end{gathered}`

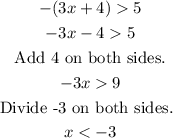
Remember the rules when dividing an inequality with a negative number. The sign will be reversed as shown above, from greater than, it became less than.

Hence, one of the possible value of x < -3.

Let's move on to the 2nd equation.

`\begin{gathered} 3x+4>5 \\ \text{Subtract 4 on both sides.} \\ 3x>1 \\ \text{Divide 3 on both sides.} \\ x>(1)/(3) \end{gathered}`

The other value of x is greater than 1/3.

To summarize, x is either less than -3 or greater than 1/3. In interval notation, we have:

`(-\infty,-3)\cup((1)/(3),\infty)`