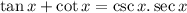
Let us change tan x and cot x to sin x and cos x
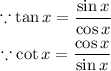
Substitute them on the left side
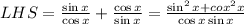
I multiplied the denominators and multiply each numerator by the opposite denominator
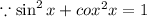
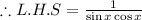
Now we will work on the right hand side
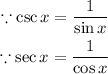
Substitute them on the right side
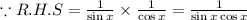
The L.H.S = R.H.S = 1/(sin x cos x)